Chapter 6 Option Values and Changing Market Conditions

Chapter 6 Option Values and Changing Market Conditions
第六章 期权价值与市场变化

Every trader who enters the marketplace must balance two opposing considerations, reward and risk. A trader hopes that his analysis of market conditions is correct, and that this will lead to profitable trading strategies. But no intelligent trader can afford to ignore the possibility of error. If he is wrong, and market conditions change in a way that adversely affects his position, how badly might the trader get hurt? A trader who fails to consider the risks associated with his position is certain to have a short and unhappy career.

每个进入市场的交易者都需要在回报和风险之间找到平衡。交易者希望自己的市场分析是正确的，从而制定出盈利的策略。但任何交易者都不能忽视可能的错误。如果市场走势对他的头寸不利，他会损失多少？忽视风险的交易者注定会有短暂且不顺利的职业生涯。

Consider the trader who goes into the marketplace and purchases a futures contract. What is he worried about? Obviously he is worried that the market will fall. Indeed, anyone who takes a position in an underlying contract has only one real concern, that the market will move in the wrong direction. If a trader has a long position, he is at risk from a decline in the market; if he has a short position, he is at risk from a rise in the market.

考虑一个进入市场购买期货合约的交易者。他担心什么？显然，他担心市场会下跌。实际上，任何在标的合约中持有头寸的交易者，唯一真正关心的就是市场朝错误方向波动。如果交易者持有多头头寸，他面临市场下跌的风险；如果持有空头头寸，则面临市场上涨的风险。

Unfortunately, the risks with which an option trader must deal are not one-dimensional. A wide variety of forces can affect an option's value. If a trader uses a theoretical pricing model to evaluate options, any of the inputs into the model can represent a risk since there is always a chance that the inputs have been incorrectly estimated. Even if the trader has correctly estimated current market conditions, it's possible that over time conditions will change in a way that will adversely affect the value of his option position. Because of the many forces affecting an option's value, prices can change in ways which may surprise even the most experienced trader. Since decisions must often be made quickly, and sometimes without the aid of a computer, much of an option trader's education consists of learning how changing market conditions are likely to change an option's value and the risks associated with an option position.

不幸的是，期权交易者面临的风险并不是单一维度的。多种因素可能影响期权的价值。如果交易者使用理论定价模型评估期权，模型中的任何输入都可能带来风险，因为这些输入值总有可能被错误估计。即使交易者正确估计了当前市场条件，随着时间推移，条件也可能发生变化，从而对期权头寸的价值产生不利影响。由于多种因素影响期权价值，价格变化可能会让即使是最有经验的交易者感到意外。因为决定往往需要迅速做出，有时甚至无法借助电脑，期权交易者的学习过程在很大程度上包括了解如何应对不断变化的市场条件及其对期权价值的影响和相关风险。

First, let's consider the general effects of changing market conditions on an option's value. These changes are summarized in Figure 6-1.

Figure 6-1: The Effect of Changing Market Conditions on an Option's Theoretical Value

If...	Call values will...	Put values will...
The price of the underlying contract rises	rise	fall
The price of the underlying contract falls	fall	rise
Volatility rises	rise	rise
Volatility falls	fall	fall
Time passes	fall*	fall*
* In some unusual cases, it may be possible for an option to rise in value as time passes. The circumstances which can cause this will be discussed later.

首先，让我们考虑市场条件变化对期权价值的一般影响。这些变化总结在图 6-1 中。

图 6-1：市场条件变化对期权理论价值的影响

如果...	看涨期权价值将...	看跌期权价值将...
标的合约价格上涨	上升	下降
标的合约价格下跌	下降	上升
波动率上升	上升	上升
波动率下降	下降	下降
时间流逝	下降*	下降*
* 在一些特殊情况下，随着时间流逝，期权价值可能会上升。导致这种情况的因素将在后续讨论。

As the price of the underlying rises or falls, options are more or less likely to finish in-the-money, and their values rise and fall accordingly. As volatility rises, extreme outcomes in the underlying contract become more likely, and this increases an option's value. As volatility falls, or as time to expiration grows shorter, extreme outcomes become less likely, and this reduces an option's value.

随着标的资产价格的涨跌，期权到期时为实值的可能性相应变化，从而导致它们的价值上涨或下跌。当波动性上升时，标的合约出现极端结果的可能性增加，这会提升期权的价值。相反，当波动性下降或到期时间缩短时，极端结果的可能性减少，这会降低期权的价值。

Note that we have not considered the effect of changes in interest rates on option values. Since interest rates affect options differently depending on the underlying instrument and the settlement procedure, it is not possible to generalize about the effect of changing interest rates. However, we can logically deduce the effect of changing interest rates on option values by thinking of a call as a substitute for purchasing the underlying contract, and a put as a substitute for selling the underlying contract. For example, suppose we want to purchase a certain stock. The alternative is to purchase a call option. If interest rates are high, we will prefer the call since the outright purchase of stock requires a much larger cash outlay, and therefore a greater carrying cost. On the other hand, if interest rates are low, the carrying cost associated with stock is not as great, and calls become a less attractive alternative to purchasing the stock. Hence, rising interest rates cause stock option calls to rise in value, and falling interest rates cause stock option calls to fall in value.

请注意，我们没有考虑利率变化对期权价值的影响。由于利率对不同标的工具和结算程序的期权影响不同，因此无法对利率变化的影响进行概括。然而，我们可以通过将看涨期权视为购买标的合约的替代品，将看跌期权视为出售标的合约的替代品，推导出利率变化对期权价值的影响。例如，假设我们想购买某只股票，另一种选择是购买看涨期权。如果利率较高，我们会更倾向于选择看涨期权，因为直接购买股票需要更多现金支出，持有成本也更高。相反，如果利率较低，股票的持有成本较小，看涨期权相对购买股票的吸引力下降。因此，利率上升会导致股票看涨期权的价值上升，而利率下降则会导致其价值下降。

The effect is just the opposite for stock option puts. If we are considering the sale of stock, the alternative is the purchase of a put. In a high interest rate environment the sale of stock will be more desirable since the cash credit resulting from the sale will earn greater interest. In a low interest rate environment puts become more attractive since the earnings on any cash credit resulting from the sale of stock is reduced. Hence, rising interest rates cause stock option puts to fall in value, and falling interest rates cause stock option puts to rise in value.

股票看跌期权的情况正好相反。如果我们考虑卖出股票，另一种选择是购买看跌期权。在高利率环境下，卖出股票更为理想，因为出售所得的现金收益能赚取更高利息。而在低利率环境下，看跌期权的吸引力增加，因为出售股票所带来的现金收益减少。因此，利率上升会导致股票看跌期权的价值下降，利率下降则会导致其价值上升。

The situation is more complex when it comes to options on foreign currencies because a trader must deal with two interest rates, a domestic rate and a foreign rate. The effect of changes in domestic interest rates will be the same as the effect on stock options: a call will avoid the cash outlay required to purchase the currency, and a put will forego the cash credit resulting from the sale of the currency. However, the effect of a change in the foreign interest rate will be just the opposite. If foreign interest rates are high, rather than purchase a call one will always prefer to purchase the currency outright in order to earn the higher interest rate. Hence, higher (lower) foreign interest rates lead to lower (higher) call values. But if foreign rates are high, a put becomes a more desirable alternative to selling the foreign currency since one will want to continue to earn a high rate on the foreign currency. Hence, higher (lower) foreign interest rates lead to higher (lower) put values.

外币期权的情况更复杂，因为交易者需要考虑两个利率：国内利率和外国利率。国内利率变化的影响与股票期权相同：看涨期权避免了购买外币所需的现金支出，而看跌期权放弃了出售外币的现金收益。然而，外国利率变化的影响则正好相反。如果外国利率较高，人们通常倾向于直接购买外币以获取更高的利息。因此，外国利率上升（下降）会导致看涨期权的价值下降（上升）。但如果外国利率较高，看跌期权就成为卖出外币的更好选择，因为人们希望继续赚取高利率。因此，外国利率上升（下降）会导致看跌期权的价值上升（下降）。

Stock and foreign currency options are always assumed to be subject to stock-type settlement (immediate cash payment for the option). But the settlement procedure for options on futures contracts may vary, depending on the exchange. Sometimes such options are settled like stock and sometimes they are settled like futures. While there is no carrying cost associated with a futures contract, there will be a carrying cost associated with an option if it is subject to stock-type settlement. In such a case, option values will fall when interest rates are high (the option becomes a less desirable alternative to a position in the futures contract) and rise when interest rates are low (the option becomes a more desirable alternative to a futures position). The effect, however, will be small since the value of the option, unless it is very deeply in-the-money, is small relative to the value of the underlying contract. Futures options are therefore much less sensitive to changes in interest rates than options on stocks and foreign currencies. When futures options are subject to futures-type settlement, changes in interest rates have no effect at all on option values since there is no carrying cost associated with either the underlying contract or the option.

股票和外币期权通常假设按股票类型结算（即期权立即以现金支付）。但期货合约的期权结算程序可能因交易所而异，有时像股票那样结算，有时像期货那样结算。期货合约没有持有成本，而按股票类型结算的期权会产生持有成本。在这种情况下，当利率较高时，期权价值会下降（因为期权作为期货合约的替代品不再吸引人）；当利率较低时，期权价值会上升（因为期权作为期货头寸的替代品更具吸引力）。然而，影响相对较小，因为期权的价值，除非非常深度实值，相对于标的合约的价值较小。因此，期货期权对利率变化的敏感性远低于股票和外币期权。当期货期权按期货类型结算时，利率变化对期权价值没有影响，因为标的合约和期权都没有持有成本。

The general effects of a change in interest rates are shown in Figure 6-2. In each case, the reader can intuitively arrive at the correct conclusion if he asks himself whether a call (put) is a better or worse substitute for the outright purchase (sale) of the underlying contract.

Figure 6-2: The Effect of Changing Interest Rates on Option Values

Interest	If Domestic Interest Rates Rise	If Domestic Interest Rates Fall	If Foreign Interest Rates Rise	If Foreign Interest Rates Fall
Calls on stock will...	rise in value	fall in value	(not applicable)	(not applicable)
Puts on stock will...	fall in value	rise in value	(not applicable)	(not applicable)
Calls on a foreign currency will...	rise in value	fall in value	fall in value	rise in value
Puts on a foreign currency will...	fall in value	rise in value	rise in value	fall in value
Calls on a futures contract will... (stock type settlement)	fall in value	rise in value	(not applicable)	(not applicable)
Puts on a futures contract will... (stock type settlement)	fall in value	rise in value	(not applicable)	(not applicable)
Calls on a futures contract will... (futures type settlement)	remain unchanged	remain unchanged	(not applicable)	(not applicable)
Puts on a futures contract will... (futures type settlement)	remain unchanged	remain unchanged	(not applicable)	(not applicable)

利率变化的一般影响如图 6-2 所示。在每种情况下，读者可以通过询问自己看涨期权（看跌期权）是否比直接购买（出售）标的合约更好或更差，从而直观地得出正确结论。

图6-2：市场利率变化对期权价值的影响

利率	如果本国利率上升	如果本国利率下降	如果外国利率上升	如果外国利率下降
股票看涨期权将会...	价值上升	价值下降	（不适用）	（不适用）
股票看跌期权将会...	价值下降	价值上升	（不适用）	（不适用）
外币看涨期权将会...	价值上升	价值下降	价值下降	价值上升
外币看跌期权将会...	价值下降	价值上升	价值上升	价值下降
期货看涨期权将会...（股票型结算）	价值下降	价值上升	（不适用）	（不适用）
期货看跌期权将会...（股票型结算）	价值下降	价值上升	（不适用）	（不适用）
期货看涨期权将会...（期货型结算）	保持不变	保持不变	（不适用）	（不适用）
期货看跌期权将会...（期货型结算）	保持不变	保持不变	（不适用）	（不适用）

The dividend which is expected to be paid on stock during the life of a stock option may also affect the value of the option. In a simple sense, we can equate a dividend payment with the foreign interest rate on a currency option. If we own the foreign currency we can earn interest on it. In the same way, if we own the stock we will receive whatever dividend is paid on the stock. If dividends increase, we will prefer to take a long position by purchasing the stock rather than purchasing a call. The call therefore becomes a less desirable alternative to owning the stock. In the case of puts, if dividends increase we will prefer to take a short position by purchasing a put rather than selling the stock, since the sale of the stock will result in the loss of the dividend. Hence, rising dividends will cause stock option calls (puts) to fall (rise) in value, and falling dividends will cause stock option calls (puts) to rise (fall) in value. This is summarized in Figure 6-3.

Figure 6-3: The Effect of Changing Dividens on Stock Options

If...	Call values will...	Put values will...
The dividend is increased	fall	rise
The dividend is decreased	rise	fall

股票期权有效期内预期支付的股息也会影响期权的价值。简单来说，股息支付可以看作是货币期权的外币利率。如果我们拥有外币，就可以从中获得利息；同样，如果我们拥有股票，就会收到股票的股息。如果股息增加，我们会更倾向于购买股票以建立多头头寸，而不是购买看涨期权，因此看涨期权的吸引力减弱。对于看跌期权，如果股息增加，我们会更倾向于购买看跌期权以建立空头头寸，而不是出售股票，因为出售股票会导致股息损失。因此，股息上升会导致股票看涨期权价值下降，而看跌期权价值上升；股息下降则会导致看涨期权价值上升，而看跌期权价值下降。这一点在图 6-3 中有所总结。

图6-3：股息变化对股票期权的影响

如果...	看涨期权将...	看跌期权将...
股息增加	下跌	上涨
股息减少	上涨	下跌

We can generalize about the effects of changing market conditions on the value of options, but we must still consider the magnitude of the changes. Will the changes be large or small, representing either a major or minor risk, or something in between?

我们可以概括市场条件变化对期权价值的影响，但仍需考虑变化的幅度。这些变化是大是小？是代表重大风险还是小风险，或是介于两者之间？

Fortunately, along with the theoretical value, pricing models also generate several other numbers which enable a trader to assess not only the direction of the change, but also the relative magnitude of the change. While these numbers will not answer all our questions concerning changing market conditions, they will help us to better assess the risks associated with both individual and complex option positions.

幸运的是，定价模型除了理论价值外，还会生成其他一些数字，使交易者能够评估变化的方向和相对幅度。虽然这些数字无法解答我们对市场条件变化的所有疑问，但它们将帮助我们更好地评估与单个和复杂期权头寸相关的风险。

THE DELTA
德尔塔（Delta）

We touched on the delta (Δ) in the last chapter as needed to determine the number of underlying contracts to option contracts required to establish a neutral hedge. The delta has several other interpretations, any of which may be useful to a trader.

在上一章中，我们提到了德尔塔（Δ），用于确定建立中性对冲所需的标的合约与期权合约的数量。德尔塔还有其他几种解释，对交易者也可能很有用。

Rate of Change
变化率

Figure 6-4 (footnote 1: In order to generalize characteristics of the option sensitivities, which in most cases are similar regardless of the type of underlying instrument, we assume an interest rate of zero in Figures 6-4 through 6-21.) shows what happens to the theoretical value of a call as the price of the underlying contract changes. Under some conditions, when the call is very deeply in-the-money, its value changes at a rate almost identical to that of the underlying. If the underlying price moves up or down one point, the call's value will change by an equal amount. Under other conditions, when the call is far out-of-the-money, its value may change only slightly, even with a large change in the price of the underlying. The delta is a measure of how an option's value changes with respect to a change in the price of the underlying contract.

图 6-4（脚注 1：为了概括期权敏感性的特征，我们假设图 6-4 至 6-21 中的利率为零，因为这些特征在大多数情况下与标的资产类型无关。）展示了标的合约价格变化时，买权（call）的理论价值如何变化。在某些情况下，当买权深度实值时，其价值变化速率几乎与标的资产相同。如果标的资产价格波动一个点，买权的价值也将相应变化一个点。而在其他情况下，当买权远离实值时，即使标的资产价格大幅波动，买权的价值可能也只会轻微变化。德尔塔（delta）用于衡量期权价值相对于标的合约价格变化的敏感度。

In theory, an option can never gain or lose value more quickly than the underlying, so the delta of a call always has an upper bound of 100. (Again, we will retain the common practice of writing the delta without the decimal point. Hence, a delta of 1.00 will be written as 100. This is sometimes referred to as the percent format.) An option with a delta of 100 will move up or down one full point for each full point move up or down in the price of the underlying. It is moving at 100% of the rate of the underlying. In theory, a call also cannot move in the opposite direction of the underlying market, so the delta of a call has a lower bound of zero. A call with a delta of zero will move negligibly, even if the underlying contract makes a relatively large move.

理论上，期权的价值不会比标的资产变化得更快，因此买权的德尔塔上限为 100。（我们将继续不带小数点书写德尔塔的惯例，因此德尔塔为 1.00 时表示为 100，这有时被称为百分比格式。）德尔塔为 100 的期权将在标的资产价格每上升或下降一个点时，自己也上升或下降一个点，其变化率为标的资产的 100%。理论上，买权无法朝与标的市场相反的方向变化，因此买权的德尔塔下限为零。德尔塔为零的买权，即使标的合约有较大波动，其自身的变化也微乎其微。

Most calls, of course, will have deltas somewhere between zero and 100 and will move at a slower rate than the underlying. A call with a delta of 25 can be expected to change its value at 25% of the rate of the underlying. If the underlying rises (falls) 1.00, the option can be expected to rise (fall) .25. A call with a delta of 75 can be expected to change its value at 75% of the rate of the underlying. If the underlying rises (falls) .60, the option can be expected to gain (lose) 45 in value. Call options which are at-the-money have delta values close to 50. They rise or fall in value at just about half the rate of the underlying.

大多数买权的德尔塔值通常介于零到 100 之间，价值变化速度慢于标的资产。德尔塔为 25 的买权，其价值会以标的资产变化速率的 25% 变化。如果标的资产上涨（下跌）1.00，期权预计上涨（下跌）0.25。而德尔塔为 75 的买权，其价值会以标的资产变化速率的 75% 变化。如果标的资产上涨（下跌）0.60，期权预计增加（减少）0.45。平值买权的德尔塔值接近 50，价值变化速度约为标的资产的一半。

Thus far our discussion of deltas has focused only on calls. Puts have characteristics similar to calls, except that put values move in the opposite direction of the underlying market. In Figure 6-5 we can see that when the underlying rises, puts lose value; when the underlying falls, puts gain value. For this reason, puts always have negative deltas, ranging from zero for far out-of-the-money puts to -100 for deeply in-the-money puts.

目前为止，我们讨论的德尔塔都集中在买权。卖权与买权特性类似，但卖权的价值变化方向与标的市场相反。图 6-5 显示，当标的资产上涨时，卖权价值下降；当标的资产下跌时，卖权价值上升。因此，卖权的德尔塔总是负值，范围从远离实值卖权的 0 到深度实值卖权的 -100。

Just like a call delta, a put's delta is a measure of the rate of change in the put's value with respect to a change in the price of the underlying, but the negative sign indicates that the change will be in the opposite direction of the underlying market. A put with a delta of -10 can be expected to change its value at 10% of the rate of the underlying, but in the opposite direction. If the underlying moves up (down) .50, the put can be expected to lose (gain) .05 in value. At-the-money puts will have deltas of approximately -50, and can be expected to change their value at approximately half the rate of the underlying, but in the opposite direction.

与买权德尔塔类似，卖权德尔塔衡量卖权价值相对于标的资产价格变化的速率，但负号表示其变化方向与标的市场相反。德尔塔为-10 的卖权，其价值会以标的资产变化速率的 10% 变化，方向相反。如果标的资产上涨（下跌）0.50，卖权预计损失（增加）0.05。平值卖权的德尔塔约为 -50，预计其价值变化速率为标的资产的一半，但方向相反。

Hedge Ratio
对冲比率

As discussed in Chapter 5, if we wish to hedge an option position against the underlying contract, the delta tells us the proper ratio of underlying contracts to options required to establish a neutral hedge. An underlying contract always has a delta of 100, so the proper hedge ratio can be determined by dividing 100 by the option's delta. An at-the-money option has a delta of 50, so the proper hedge ratio is 100/50, or 2/1. For every two options purchased, we need to sell one underlying contract to establish a neutral hedge. A call with a delta of 40 requires the sale of two underlying contracts for each five options purchased, since 100/40 = 5/2.

如第 5 章所述，如果我们希望对冲期权头寸与标的合约之间的风险，德尔塔能告诉我们需要多少标的合约与期权的比例，以建立一个中性对冲。标的合约的德尔塔总是 100，因此合适的对冲比率可以通过用 100 除以期权的德尔塔来确定。平值期权的德尔塔为 50，因此合适的对冲比率是 100/50，或 2:1。也就是说，每买入两个期权，我们需要卖出一个标的合约以建立中性对冲。德尔塔为 40 的买权需要为每买入五个期权卖出两个标的合约，因为 100/40 = 5/2。

Since puts have negative deltas, the purchase of puts will require us to hedge the position by purchasing underlying contracts. A put with a delta of -75 will require the purchase of three underlying contracts for each four puts purchased, since 100/75 = 4/3.

由于卖权的德尔塔为负值，买入卖权需要通过买入标的合约来对冲。德尔塔为 -75 的卖权需要为每买入四个卖权买入三个标的合约，因为 100/75 = 4/3。

Thus far, all the hedges we have looked at have consisted of options and underlying contracts. But any hedge, whether options versus underlying contracts, or options versus options, is delta neutral as long as all the deltas in the hedge add up to zero. For example, suppose we buy four calls with a delta of 50 each, and ten puts with a delta of -20 each. Our position is delta neutral since (+4× +50) + (+10 x-20) = 0. A position can be highly complex, consisting of underlying contracts, calls, and puts, with different exercise prices and expiration dates, but as long as the deltas add up to approximately zero we say that the position is delta neutral.

到目前为止，我们讨论的对冲都由期权与标的合约组成。但无论是期权对标的合约的对冲，还是期权对期权的对冲，只要所有对冲中的德尔塔总和为零，该对冲就是德尔塔中性。例如，假设我们买入四个德尔塔为 50 的买权和十个德尔塔为 -20 的卖权。我们的头寸是德尔塔中性的，因为 (+4× +50) + (+10× -20) = 0。一个头寸可以非常复杂，包含标的合约、买权和卖权，且具有不同的行权价和到期日，但只要德尔塔加起来接近零，我们就认为该头寸是德尔塔中性的。

Theoretical or Equivalent Underlying Position
理论或等效标的头寸

Many option traders come to the option market after trading in the underlying instruments. Futures option traders often start their careers by trading futures contracts; stock option traders often start by trading stock. If a trader has become accustomed to evaluating his risk in terms of the number of underlying contracts bought or sold (either futures contracts or shares of stock), he can use the delta to equate the directional risk of an option position with a position of similar size in the underlying market.

许多期权交易者在进入期权市场前，通常已有标的合约的交易经验。期货期权交易者常从期货合约交易开始，股票期权交易者则常从股票交易入门。如果交易者习惯用买卖标的合约的数量（无论是期货合约还是股票）来评估风险，那么他可以通过德尔塔将期权头寸的方向性风险等同于标的市场中类似规模的头寸。

Since an underlying contract always has a delta of 100, each 100 deltas in an option position represents a theoretical position equivalent to one underlying contract. A trader Who owns an option with a delta of 50 is long, or controls, approximately ½ of an underlying contract. If he owns ten such contracts, he is long 500 deltas or, in equivalent terms, five underlying contracts. If the underlying is a futures contract, he is theoretically long five such contracts. If the underlying is a stock contract consisting of 100 shares of stock, he is theoretically long 500 shares of stock. The trader has a similar theoretical position if he sells 20 puts with a delta of -25 each, since -20 x-25 = +500.

由于标的合约的德尔塔始终为 100，因此期权头寸中的每 100 个德尔塔相当于一个标的合约的理论头寸。拥有德尔塔为 50 的期权，相当于控制约半个标的合约。如果他拥有 10 个这样的期权，就持有 500 个德尔塔，或等效于 5 个标的合约。如果标的是期货合约，他理论上持有 5 个这样的期货合约。如果标的是 100 股的股票合约，他理论上持有 500 股股票。同样地，若卖出 20 个德尔塔为 -25 的卖权，其理论头寸为 -20 × -25 = +500。

It is important to emphasize the theoretical aspect of the delta interpretation as an equivalent to an underlying position. An option is not simply a surrogate for an underlying position. An actual underlying position is almost exclusively sensitive to directional moves in the underlying market. An option position, while also sensitive to directional moves, is also sensitive to other changes in market conditions. An option trader who looks only at his delta position may be ignoring other risks which could have a far greater impact on his option position. He must realize that the delta represents an equivalent underlying position only under very narrowly defined market conditions.

需要强调的是，德尔塔作为等效标的头寸的解释是理论性的。期权并不等同于标的头寸。标的头寸几乎只受标的市场方向波动的影响，而期权头寸除了对方向波动敏感，还会受其他市场条件变化的影响。若交易者仅关注自己的德尔塔头寸，可能会忽略对其期权头寸影响更大的其他风险。必须明白，德尔塔仅在特定的市场条件下才可视为等效标的头寸。

The reader may have already noted that our three interpretations of delta-the hedge ratio, the rate of change in the theoretical value, and the equivalent underlying position-are all essentially the same. How a trader interprets a delta position depends primarily on his trading strategy. For example, suppose a trader has a delta position of +500. If the trader intends to maintain a delta neutral position, he must sell five underlying contracts (the hedge ratio interpretation). However, if he believes the market will rise and wants to maintain his delta position, he knows that in theory he is long five underlying contracts (the equivalent underlying position interpretation). And finally, if he does maintain his delta position of +500, the value of his position will change at five times the rate, or 500%, of the underlying market (the rate of change interpretation). Even though a trader may interpret the delta differently at different times, each interpretation is mathematically the same.

读者或许已经注意到，我们对德尔塔的三种解释——对冲比率、理论价值变化率和等效标的头寸——实质上是一致的。交易者如何解读德尔塔头寸，主要取决于其交易策略。例如，假设某交易者的德尔塔头寸为 +500。如果他想保持德尔塔中性头寸，需要卖出五个标的合约（对冲比率的解释）。但如果他认为市场会涨并想保留德尔塔头寸，则可以理解为理论上持有五个标的合约（等效标的头寸的解释）。最后，如果他维持 +500 的德尔塔头寸，头寸价值将以标的市场五倍的速度变化，即 500%（变化率的解释）。虽然交易者在不同情境下对德尔塔的解读不同，但这些解释在数学上是等同的。

There is one other interpretation of the delta which is perhaps of less practical use but may still be worth mentioning. If we ignore the sign of the delta (positive for calls, negative for puts), the delta is approximately equal to the probability that the option will finish in-the-money. A call with a delta of 25, or a put with a delta of -25, has approximately a 25% chance of finishing in-the-money. A call with a delta of 75, or a put with a delta of -75, has approximately a 75% chance of finishing in-the-money. As an option's delta moves closer to 100, or -100 for puts, the option becomes more and more likely to finish in-the-money. As the delta moves closer to zero, the option becomes less and less likely to finish in-the-money. We can also see why at-the-money options have deltas close to 50. If we assume that price changes are random, there is half a chance that the market will rise (the option goes into-the-money), and half a chance that the market will fall (the option goes out-of-the money).

还有一种对德尔塔的解释，虽然实用性较低，但仍值得一提。如果忽略德尔塔的正负号（认购期权为正，认沽期权为负），德尔塔大致等于期权最终进入实值的概率。德尔塔为 25 的认购期权或德尔塔为 -25 的认沽期权，大约有 25% 的概率进入实值。德尔塔为 75 的认购期权或德尔塔为 -75 的认沽期权，则大约有 75% 的概率进入实值。随着德尔塔接近 100（认沽期权为 -100），期权进入实值的概率越来越大；而当德尔塔接近零时，期权进入实值的概率越来越小。这也解释了为何平值期权的德尔塔通常接近 50。若假设价格变动是随机的，市场上涨（期权进入实值）或下跌（期权变为虚值）的概率各为一半。

Of course, the delta is only an approximation of the probability since interest rate considerations and, in the case of stock options, dividends, may distort this interpretation. Moreover, most option strategies depend not only on whether an option finishes in-the-money, but by how much. If a trader sells an option with a delta of 10 in the belief that the option will expire worthless nine times out of ten, he may indeed be correct. But if on the tenth time he loses an amount greater than the total premium he took in the nine times the option expired worthless, the trade will result in a negative expected return. In option trading the primary consideration is not always how often a strategy wins or loses, but also how much it wins or loses. Every experienced trader is willing to accept several small losses if he can occasionally offset these with one big win.

当然，德尔塔只是概率的近似值，因为利率因素以及股票期权中的股息可能会影响这一解释。此外，大多数期权策略不仅仅取决于期权是否进入实值，还取决于进入实值的程度。如果交易者卖出一个德尔塔为 10 的期权，并认为该期权十次中有九次会变为无值而过期，他的判断可能是对的。但如果第十次的损失超过前九次获得的总权利金，那么这笔交易的预期回报将是负数。在期权交易中，关键不仅是策略胜负的次数，还要看赢或输的幅度。每个有经验的交易者都愿意接受几次小额损失，只要能偶尔通过一次大额盈利弥补这些损失。

THE GAMMA
伽马（Gamma）

In discussing the delta, we noted that under some circumstances, when the option is far out-of-the-money, its delta is close to zero. At other times, when the option is deeply in-the-money, its delta is close to 100 (-100 for puts). We can logically conclude that as the underlying price changes, the delta of an option must also be changing. As the underlying price rises, call deltas move towards 100 and put deltas move towards zero; as the underlying price falls, call deltas move towards zero and put deltas move towards -100. This effect is shown in Figures 6-6 and 6-7.

在讨论德尔塔时，我们提到在某些情况下，当期权深度虚值时，其德尔塔接近零；而在另一些情况下，当期权深度实值时，其德尔塔接近 100（对于看跌期权为 -100）。因此，我们可以得出结论，随着标的资产价格的变化，期权的德尔塔也会随之变化。当标的资产价格上升时，看涨期权的德尔塔向 100 移动，看跌期权的德尔塔向零移动；当标的资产价格下降时，看涨期权的德尔塔向零移动，看跌期权的德尔塔向 -100 移动。此效应在图 6-6 和图 6-7 中展示。

The gamma (Γ), sometimes referred to as the curvature of an option, is the rate at which an option's delta changes as the price of the underlying changes. The gamma is usually expressed in deltas gained or lost per one point change in the underlying, with the delta increasing by the amount of the gamma when the underlying rises, and falling by the amount of the gamma when the underlying falls. If an option has a gamma of 5, (footnote 2: When the delta is expressed in the decimal format (0 to 1.00), the gamma is expressed in the same) for each point rise (fall) in the price of the underlying, the option will gain (lose) 5 deltas. If the option originally had a delta of 25, and the underlying moves up (down) one full point, then the new delta of the option will be 30 (20). If the underlying moves up (down) another point, the new delta will be 35 (15).

伽马（Γ），有时称为期权的曲率，是期权的德尔塔随标的资产价格变化而变化的速率。伽马通常以每单位标的资产价格变动所获得或失去的德尔塔表示。当标的资产价格上涨时，德尔塔增加相应的伽马值；当标的资产价格下跌时，德尔塔减少相应的伽马值。如果某个期权的伽马为 5（脚注 2：当德尔塔以小数形式（0 到 1.00）表示时，伽马也以相同方式表示），那么当标的资产价格每上涨（下跌）一个点时，期权的德尔塔将增加（减少）5。如果该期权最初的德尔塔为 25，而标的资产上升（下降）一个完整的点，则期权的新德尔塔为 30（20）。如果标的资产再上升（下降）一个点，新的德尔塔将变为 35（15）。

Note that Figures 6-6 and 6-7 seem to be identical, even though the former represents call gammas and the latter put gammas. This can only mean that both calls and puts with the same exercise price and the same amount of time to expiration have the same curvature. (footnote 3: If interest rates are zero, as they are assumed to be in Figures 6-6 and 6-7, the gamma of calls and puts with the same exercise price will be identical. If interest rates are not zero, and there is a possibility of early exercise, the gammas may differ slightly.) This may at first seem odd, but it becomes logical when we remember that zero is greater than -50 in the same way that -50 is greater than -100. Negative numbers become more positive (or less negative) as one moves towards zero. Therefore, both calls and puts must have positive gammas. This often confuses the new trader since, through his use of the delta, he is accustomed to associating positive numbers with calls and negative numbers with puts. But regardless of whether we are working with calls or puts, we always add the gamma to the old delta as the underlying rises, and subtract the gamma from the old delta as the underlying falls. When a trader is long options, whether calls or puts, he has a long gamma position. When he is short options, he has a short gamma position.

请注意，图 6-6 和图 6-7 看似相同，尽管前者代表看涨期权的伽马，后者代表看跌期权的伽马。这意味着相同行权价和到期时间的看涨和看跌期权有相同的曲率。（脚注 3：如果利率为零，如图 6-6 和图 6-7 所示，看涨和看跌期权的伽马相同。如果利率不为零且存在提前行权的可能性，伽马可能会稍有不同。）这看似奇怪，但实际上，当我们理解 0 大于 -50，而 -50 又大于 -100 时，这就变得合乎逻辑了。负数在接近 0 时会变得更正（或更少负），因此看涨和看跌期权都必须有正伽马。这一点经常让新手交易员困惑，因为他们通常把正数与看涨期权，负数与看跌期权联系起来。但无论是看涨还是看跌期权，当标的资产上涨时，我们总是将伽马加到原来的德尔塔上，标的资产下跌时，我们则减去伽马。当交易员持有期权时，无论是看涨还是看跌期权，他都是 “多伽马” 状态；反之，卖出期权时就是 “空伽马” 状态。

For example, suppose an at-the-money call, with a delta of 50, and an at-the-money put, with a delta of -50, both have gammas of 5. If the underlying contract rises one point, we add the gamma of 5 to the call delta of 50, to get the new delta of 55. To get the new put delta if the underlying contract rises one point we also add the gamma of 5 to the put delta of -50 to get the new delta of -45. This corresponds to our intuition that as the underlying price rises, at-the-money calls move into-the-money and at-the-money puts move out-of-the-money. If the underlying contract falls one full point, in both cases we subtract the gamma, giving the call a delta of 45 (50-5), and the put a delta of -55 (-50-5). Now the call is moving out-of-the-money and the put is moving into-the-money.

例如，假设一个平值看涨期权的德尔塔为 50，平值看跌期权的德尔塔为 -50，它们的伽马均为 5。如果标的资产上涨一个点，我们将伽马 5 加到看涨期权的德尔塔上，得到新的德尔塔为 55。同样，标的资产上涨一个点时，我们也将伽马 5 加到看跌期权的德尔塔上，得到新的德尔塔为 -45。这与我们的直觉一致：当标的资产价格上涨时，平值看涨期权变为实值，平值看跌期权变为虚值。如果标的资产下跌一个点，伽马从两者的德尔塔中减去，得到看涨期权的德尔塔为 45（50-5），看跌期权的德尔塔为 -55（-50-5）。此时，看涨期权变为虚值，看跌期权变为实值。

We know that an underlying contract has a delta of 100. But what is the gamma associated with an underlying contract? Since the gamma is the rate of change in the delta, and the delta of an underlying contract is always 100, the gamma must be zero.

我们知道标的资产的德尔塔为 100，那么它的伽马是多少呢？由于伽马表示德尔塔的变化率，而标的资产的德尔塔始终为 100，因此伽马为零。

The gamma is a measure of how fast an option changes its directional characteristics, acting more or less like an actual underlying position. Since directional risk is always important, the gamma is an important risk measurement. Indeed, an option position can change its directional risk dramatically, even if a trader takes no action in the marketplace. A large gamma number, whether positive or negative, indicates a high degree of risk; a low gamma number indicates a low degree of risk. Every option trader learns to look carefully not only at current directional risk (the delta), but also at how that directional risk will change if the underlying market begins to move (the gamma).

伽马衡量的是期权在方向性上的变化速度，即期权的表现是否越来越像一个实际的标的资产。由于方向性风险始终很重要，伽马是一个关键的风险衡量指标。事实上，即使交易员不在市场上采取任何行动，期权头寸的方向性风险也可能发生剧烈变化。无论是正伽马还是负伽马，数值越大意味着风险越高；伽马数值越小，风险越低。每个期权交易员都需要仔细关注不仅当前的方向性风险（德尔塔），还要关注当标的市场开始波动时方向性风险的变化（伽马）。

Consider a trader who sells ten calls with a delta of 30 each. He is short 300 deltas (-10 × 30), equivalent in theory to being short three underlying contracts. If this trader is accustomed to dealing in lots of five underlying contracts or less, he is, for the moment, within his normal risk limits. If the market rises ten points and he considers only his original delta position of -300, he may assume that he is still, in theory, short the same three underlying contracts. But what if the initial gamma of each call was 6? Then, for each point rise in the underlying contract, each call will gain o deltas. When the underlying rises ten points, each call will gain 60 deltas, for a total delta of 90 each. The trader's directional risk has now increased by a factor of three. Instead of the initial delta of -300, the delta position is now -900, well beyond his normal risk limits.

举个例子，假设某交易员卖出了 10 张德尔塔为 30 的看涨期权。他的德尔塔头寸为 -300（-10 × 30），理论上相当于做空了 3 份标的合约。假设他习惯于管理最多 5 份标的合约的风险，目前他仍在正常的风险范围内。然而，若市场上涨 10 点，且他只考虑原始的 -300 德尔塔头寸，可能会误以为自己仍然在做空 3 份标的合约。但如果每张期权的初始伽马为 6，那么每张期权在标的上涨 1 点时将增加 6 个德尔塔。随着标的上涨 10 点，每张期权将增加 60 个德尔塔，总德尔塔达到 90 个。此时，这位交易员的方向性风险增加了 3 倍，德尔塔头寸从最初的 -300 变为 -900，远远超出了他的正常风险范围。

A large gamma can sometimes overwhelm the inexperienced trader. New traders are well advised to avoid large gamma positions, particularly negative ones, because of the speed with which such positions can change. Even experienced traders occasionally take on gamma positions which are too risky. This was dramatically demonstrated in the collapse of the Volume Investors clearing firm on the COMEX in the spring of 1985. Several traders, all clearing their trades through the same firm, built up extremely large negative gamma positions by selling large numbers of out-of-the-money gold options. In the past this had been a very profitable strategy, since the gold market had been relatively quiet with low volatility. But on this occasion the market made a violent upward move, leaving the traders, who had originally been delta neutral, short thousands of deltas in a rapidly rising market. The losses sustained by the traders not only led to the collapse of the clearing firm, but also to a crisis in the COMEX's clearing association. The incident might have been avoided had someone, either the traders themselves, the clearing firm, or the clearing association, realized that the large negative gamma position represented an unacceptable risk. Most firms which trade options or clear option trades for their customers now have risk managers responsible for identifying such dangerous positions.

高伽马有时会让缺乏经验的交易员措手不及。新手应尽量避免持有高伽马头寸，尤其是负伽马头寸，因为这些头寸变化速度非常快。即使是有经验的交易员，有时也会承担过大的伽马风险。1985 年春季，COMEX 交易所的 Volume Investors 清算公司倒闭，生动展示了这一风险。一些交易员通过这家清算公司，建立了大量负伽马头寸，卖出了大量虚值黄金期权。在过去，由于黄金市场波动较小，这一策略曾非常成功。然而，这次市场突然暴涨，导致这些原本德尔塔中性的交易员，迅速变成了数千个德尔塔的空头，面对快速上涨的市场。交易员的损失不仅导致清算公司倒闭，还引发了 COMEX 清算协会的危机。如果当时有人——无论是交易员、清算公司，还是清算协会——认识到这个大规模负伽马头寸的巨大风险，事件本可避免。如今，大多数从事期权交易或为客户清算期权交易的公司，都会配备风险管理人员，专门负责识别这些危险的头寸。

The gamma can also help a trader maintain a delta neutral position by enabling him to make a quick estimate of how the delta is changing. Suppose a trader has a delta position of +500 prior to the opening of the market. If he wishes to be delta neutral he knows that he will have to sell 500 deltas on the opening. He can accomplish this by selling five underlying contracts. But suppose that his gamma position is +100 and the market is expected to open two points higher. If it does in fact open two points higher his delta position will no longer be +500, but +700 since he will become 100 deltas longer for each point rise in the underlying. He now knows that in order to be delta neutral he must sell 700 deltas, or seven underlying contracts. He can make this calculation without any computer assistance simply by knowing his initial delta and gamma positions.

伽马可以帮助交易员快速估算德尔塔的变化，维持德尔塔中性头寸。假设交易员在开盘前持有 +500 的德尔塔头寸，如果他想保持德尔塔中性，开盘时需要卖出 500 个德尔塔，可以通过卖出 5 份标的合约实现。但如果他的伽马头寸是 +100，并且预计市场会上涨两点，那么实际开盘时他的德尔塔头寸将变为 +700，因为标的价格每上涨一点，德尔塔就增加 100。他现在知道，为了保持德尔塔中性，他需要卖出 700 个德尔塔，也就是 7 份标的合约。通过掌握初始德尔塔和伽马头寸，交易员无需借助计算机就能完成这个计算。

Since the delta of an option must always remain in the range of zero to 100 (zero to -100 for puts), we can logically conclude that the gamma must also be changing. Otherwise, continuously adding or subtracting a constant gamma would take the delta beyond this range. The effect of changes in market conditions on the value of gammas is shown in Figures 6-8, 6-9, and 6-10. Figure 6-8 demonstrates that the gamma is greatest for an option which is at-the-money, and becomes progressively smaller as an option moves either into or out-of-the-money. Figures 6-9 and 6-10 show that the gamma of an at-the-money option can increase dramatically as expiration approaches, or as we decrease our volatility assumption. A trader's gamma position, which may have initially been small, can become increasingly large through the passage of time or through changes in volatility. An option position must always be monitored to ensure that its risk characteristics remain within acceptable limits.

由于期权的德尔塔始终在 0 到 100 之间（看跌期权在 0 到 -100 之间），我们可以推断伽马也在不断变化，否则持续增加或减少固定的伽马会使德尔塔超出这个范围。市场条件变化对伽马值的影响在图 6-8、6-9 和 6-10 中展示。图 6-8 表明，伽马在期权处于平值时最大，随着期权进入或偏离实值，伽马逐渐减小。图 6-9 和图 6-10 显示，平值期权的伽马会在到期日临近或波动率降低时显著增加。交易员的伽马头寸最初可能较小，但随着时间推移或波动率变化可能变得越来越大。因此，必须时刻监控期权头寸，确保其风险特征保持在可接受范围内。

While the gamma is perhaps the most common measure of the change in the delta, the delta is also subject to change from market conditions other than movement in the price of the underlying contract. Figures 6-11 and 6-12 show how call and put deltas change as time passes. Figures 6-13 and 6-14 show how deltas change with changes in volatility. Note that all four sets of graphs have the same shape. As we increase the time to expiration or increase volatility, all options tend to become more at-the-money, with call deltas approaching 50 and put deltas approaching -50. Conversely, as we decrease the amount of time to expiration or decrease volatility, all option deltas move away from 50 (-50 for puts). An option which is in the-money will move further into-the-money, and an option which is out-of-the-money will move further out-of-the-money. Options which are at-the-money and have deltas close to 50 tend to maintain the same delta characteristics regardless of changes in time or volatility.

虽然伽马可能是德尔塔变化的最常用度量，但德尔塔也会受到其他市场条件的影响，而不仅仅是基础合约价格的波动。图 6-11 和 6-12 展示了随着时间推移，看涨和看跌期权的德尔塔如何变化。图 6-13 和 6-14 则展示了德尔塔如何随着波动率的变化而变化。值得注意的是，这四组图形的形状相同。随着到期时间的增加或波动率的上升，所有期权倾向于更接近平值，导致看涨期权的德尔塔接近 50，看跌期权的德尔塔接近 -50。相反，当到期时间减少或波动率下降时，所有期权的德尔塔都会远离 50（看跌期权为 -50）。实值期权会进一步变为实值，而虚值期权会进一步变为虚值。处于平值且德尔塔接近 50 的期权，通常在时间或波动率变化时保持相同的德尔塔特征。

Perhaps a comment is in order here about what at-the-money means. Traders tend to think of an at-the-money option as one whose exercise price is approximately equal to the current price of the underlying contract. By this definition a trader will instinctively assign a delta of 50 to any option whose exercise price is currently at-the-money. However, a theoretical pricing model will interpret the at-the-money option (the one with a delta of 50) as the option whose current exercise price is most likely to be closest to the price of the underlying contract at expiration. Suppose that interest rates are 12% annually and that a certain stock is currently trading at $100. If two five-month calls are available with exercise prices of 100 and 105, which call has a delta closer to 50? We saw in Chapter 4 that the mean of the distribution assumed in most theoretical pricing models is the forward price (the break-even price) for the underlying contract. In our present case, the forward price is the current stock price of $100 plus the $5 carrying costs over the five-month holding period. The 105 call is therefore the one which the model interprets as being at-the-money, and hence will have a delta of 50. Depending on the type of underlying contract, under extreme interest rate conditions or with a great deal of time remaining to expiration, options can have deltas decidedly different from what we might instinctively surmise.

这里需要对 “平值” 进行一些说明。交易者通常将平值期权视为其行权价格与当前基础合约价格大致相等的期权。因此，交易者本能地会将任何当前处于平值的期权的德尔塔视为 50。然而，理论定价模型会将平值期权（即德尔塔为 50 的期权）解释为在到期时其行权价格最有可能接近基础合约价格的期权。假设年利率为 12%，某股票当前交易价格为 100 美元。如果有两个行权价格分别为 100 美元和 105 美元的五个月看涨期权，哪个期权的德尔塔更接近 50？我们在第四章中看到，大多数理论定价模型中假设的分布均值是基础合约的远期价格（盈亏平衡价格）。在这个例子中，远期价格是当前股票价格 100 美元加上五个月持有期的 5 美元持有成本。因此，105 美元的看涨期权被模型视为平值期权，其德尔塔为 50。根据基础合约的类型，在极端利率条件下或距离到期还有很长时间时，期权的德尔塔可能与我们直觉猜测的相差甚远。

Just as a delta neutral option position can become unbalanced through movement in the underlying contract, it can also become unbalanced through the passage of time or through changes in volatility. No trader knows for certain whether he is delta neutral because he can't be certain about the accuracy of the inputs into the theoretical pricing model. The delta value depends, among other factors, on the volatility assumption. And volatility is just that, an assumption. A trader who sells four calls, each with a delta of 25, and buys one underlying contract, might believe that he is delta neutral. But in order to arrive at a call delta of 25 the trader is required to feed some volatility into a theoretical pricing model. If he subsequently decides that his original volatility assumption was too low, and he now raises it, we can see in Figure 6-13 that the call delta will rise towards 50. Using his new volatility assumption the delta of the call might be 35, and instead of being delta neutral, the trader is now 40 deltas short. All he did to unbalance his delta position was to change his assumptions about market conditions.

正如德尔塔中性期权头寸可以因标的合约的波动而失衡，它也可以因时间推移或波动性变化而失衡。交易者无法确切知道自己是否处于德尔塔中性状态，因为他无法确定理论定价模型输入参数的准确性。德尔塔值依赖于多种因素，包括波动率假设，而波动率本质上是一种假设。例如，一个交易者卖出四个每个德尔塔为 25 的看涨期权，并买入一个标的合约，可能认为自己处于德尔塔中性状态。但为了得出德尔塔为 25 的看涨期权，交易者需要将某种波动率输入理论定价模型。如果他随后认为原先的波动率假设过低并提高它，我们可以在图 6-13 中看到，看涨期权的德尔塔将上升至 50。根据新的波动率假设，该看涨期权的德尔塔可能为 35，这样一来，交易者实际上是 40 个德尔塔的空头，而非处于德尔塔中性状态。他所做的仅是改变了对市场状况的假设，导致德尔塔头寸失衡。

Nothing in the foregoing discussion invalidates the concept of delta neutrality, which is still an important one. However, a trader must realize that a delta neutral position depends on an estimate of market conditions, both current and future, and there is no guarantee that this estimate will be correct. As he changes his assumptions about market conditions, he must constantly change his trading strategies to fit these new assumptions. Delta neutral trading is only one aspect of this principle.

上述讨论并不否定德尔塔中性概念的重要性。然而，交易者必须意识到，德尔塔中性头寸依赖于对当前和未来市场状况的估计，而没有保证这一估计会是正确的。随着他对市场状况假设的变化，必须不断调整交易策略以适应这些新假设。德尔塔中性交易只是这一原则的一个方面。

THE THETA
西塔值（Theta）

The effect of a change in time to expiration on the theoretical values of calls and puts is shown in Figures 6-15 and 6-16. Note that all options, both calls and puts, lose value as expiration approaches. The theta (θ), or time decay factor, is the rate at which an option loses value as time passes. It is usually expressed in points lost per day, when all other conditions remain the same. An option with a theta of .05 will lose .05 in value for each day that passes with no change in other market conditions. If the option is worth 2.75 today, then tomorrow it will be worth 2.70. The day after that, it will be worth 2.65.

时间到期变化对看涨期权和看跌期权理论价值的影响如图 6-15 和图 6-16 所示。注意，随着到期日的临近，所有期权（包括看涨期权和看跌期权）都会失去价值。西塔值（θ）或时间衰减因子是期权随着时间推移而失去价值的速率。通常用每天损失的点数表示，前提是其他条件不变。一个西塔值为 0.05 的期权在其他市场条件不变的情况下，每经过一天将损失 0.05 的价值。如果该期权今天的价值为 2.75，则明天的价值将为 2.70。再过一天，它的价值将变为 2.65。

Time runs in only one direction and, technically, the theta is a positive number. However, as a convenient notation, and to remind the user that the theta represents a loss in the option's value as time passes, it is sometimes written as a negative number. This is the convention which will be followed in this text. Therefore, the theta of an option which loses .05 per day will be written as -.05. Consequently, a long option position will always have a negative theta, and a short option position will always have a positive theta. Note that this is just the opposite of the gamma, where a long option position has a positive gamma, and a short option position has a negative gamma.

时间只朝一个方向流逝，从技术上讲，西塔是一个正数。然而，为了方便起见，并提醒用户西塔表示随着时间推移期权价值的损失，它有时会写成负数。这是本文采用的约定。因此，每天损失 0.05 的期权西塔将写作 -0.05。由此，持有期权的多头头寸总是会有负的西塔，而卖出期权的空头头寸则总是会有正的西塔。请注意，这与伽马正好相反，持有期权的多头头寸有正的伽马，而卖出期权的空头头寸有负的伽马。

As a general principle, an option position will have a gamma and theta of opposite signs. Moreover, the relative size of the gamma and theta will correlate. A large positive gamma goes hand in hand with a large negative theta, while a large negative gamma goes hand in hand with a large positive theta. We saw that as expiration approaches, the gamma of an at-the-money option becomes increasingly large. The same is also true of the theta. As we get closer to expiration the rate at which an option decays begins to accelerate. If the option is exactly at-the-money, its theta at the moment of expiration becomes infinitely large.

一般来说，期权头寸的伽马和西塔符号相反。此外，伽马和西塔的相对大小也相关。较大的正伽马通常伴随较大的负西塔，而较大的负伽马则伴随较大的正西塔。随着到期日的临近，平价期权的伽马和西塔都会变得越来越大。随着到期日的逼近，期权的价值衰减速度开始加快。如果期权恰好平价，那么在到期时，它的西塔将变得无比巨大。

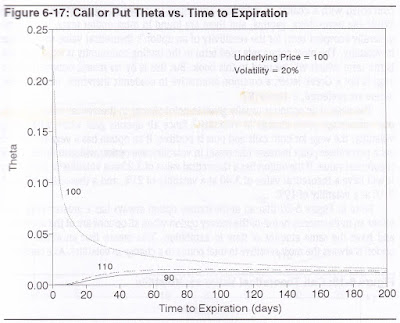
Every option position is a tradeoff between market movement and time decay. If price movement in the underlying contract will help a trader (positive gamma), the passage of time will hurt (negative theta). And vice versa. The trader can't have it both ways. Either he wants the market to move, or he wants it to sit still. This opposing effect can be seen in Figure 6-9 (gamma vs. time to expiration) and Figure 6-17 (theta vs. time to expiration). As the gamma becomes large, so does the theta. Just as a large negative gamma represents a high degree of risk with respect to market movement, a large negative theta represents a high degree of risk with respect to the passage of time.

每个期权头寸都是市场波动与时间衰减之间的权衡。如果标的合约的价格波动对交易者有利（正伽马），时间流逝则会带来损失（负西塔），反之亦然。交易者无法兼得。他要么希望市场波动，要么希望市场保持不变。这种对立效应可在图 6-9（伽马与到期时间）和图 6-17（西塔与到期时间）中看到。随着伽马增大，西塔也随之增大。较大的负伽马在市场波动方面代表了高风险，而较大的负西塔在时间流逝方面同样表示高风险。

Is it ever possible for an option to have a positive theta such that if nothing changes the option will be worth more tomorrow than it is today? When futures options are subject to stock-type settlement, as they currently are in the United States, the carrying cost on a deeply in-the-money option, either a call or a put, can, under some circumstances, be greater than the volatility component. If this happens, and the option is European (no early exercise permitted), it will have a theoretical value less than parity (less than intrinsic value). As expiration approaches, the value of the option will slowly rise to parity. Hence, the option will have a positive theta. A put option on stock can be similarly affected if the put is deeply in-the-money and, again, no early exercise is permitted. If interest rates are high enough, the put may be worth less than parity, and so will rise to parity as expiration approaches. In both cases, however, the option must be European. American options, where early exercise is a possibility, can never be worth less than parity, and so can never have positive thetas. (footnote 4: One can argue that a put on a stock which is about to pay a large dividend will also have a positive theta. When the stock gives up the dividend, it will drop by approximately the amount of the dividend, and this drop in price will increase the value of the put. The reader can make his own decision as to whether this reflects a positive theta, or is actually the result of some change in market conditions (the stock going ex-dividend).) Since the conditions under which a European option will have a positive theta are rare, in general we can assume that an option will lose value as time passes.

期权是否可能在没有变化的情况下拥有正西塔，使得明天的价值比今天更高？在美国，当期货期权采用类似股票的结算方式时，深度实值的期权（包括看涨和看跌）在某些情况下，其持有成本可能大于波动率成分。在这种情况下，如果期权是欧式期权（不允许提前行权），其理论价值将低于平价（低于内在价值）。随着到期日的临近，期权的价值会缓慢上升至平价，因此会拥有正西塔。深度实值的看跌期权也可能受到类似影响，前提是不能提前行权。如果利率足够高，看跌期权的价值可能低于平价，并会在到期时上升至平价。然而，这两种情况都要求期权是欧式的。美式期权由于可以提前行权，永远不会低于平价，因此无法拥有正西塔。（脚注 4：有人认为，即将派发大额股息的股票的看跌期权也会有正西塔。股票在派发股息后，其价格会下降大约与股息相等的金额，这一价格下跌会提高看跌期权的价值。读者可以自行判断这是否反映出正西塔，或是市场条件变化（股票除息）的结果。）由于欧式期权拥有正西塔的情况很少见，因此一般可以认为期权随着时间推移会贬值。

THE VEGA OR KAPPA
维加或卡帕

Just as we are concerned with the effect on an option's theoretical value by movement in the underlying contract (delta) and the passage of time (theta), we must also be concerned with a change in volatility. This effect is shown in Figures 6-18 and 6-19.

除了关注标的资产价格波动（德尔塔）和时间流逝（西塔）对期权理论价值的影响外，我们还必须关注波动性变化的影响。该效应在图 6-18 和图 6-19 中展示。

While the terms delta, gamma, and theta are found in most option texts, there is no generally accepted term for the sensitivity of an option's theoretical value to a change in volatility. The most commonly used term in the trading community is vega, and this is the term which will be used in this book. But this is by no means universal. Since vega is not a Greek letter, a common alternative in academic literature, where Greek letters are preferred, is kappa (K).

尽管大多数期权书籍中都提到德尔塔、伽马和西塔，但并没有一个普遍接受的术语来表示期权理论价值对波动性变化的敏感性。在交易界，最常用的术语是 “维加”，这也是本书中使用的术语。然而，这并不是普遍适用的。由于维加不是希腊字母，因此在学术文献中，常见的替代词是 “卡帕”（K），因为希腊字母在这些文献中更受欢迎。

The vega of an option is usually given in point change in theoretical value for each one percentage point change in volatility. Since all options gain value with rising volatility, the vega for both calls and puts is positive. If an option has a vega of .15, for each percentage point increase (decrease) in volatility, the option will gain (lose) .15 in theoretical value. If the option has a theoretical value of 3.25 at a volatility of 20%, then it will have a theoretical value of 3.40 at a volatility of 21%, and a theoretical value of 3.10 at a volatility of 19%.

期权的维加通常表示每增加一个百分点的波动性所导致的理论价值的点数变化。由于所有期权在波动性上升时都会增值，因此无论是看涨期权还是看跌期权，其维加都是正值。如果某个期权的维加为 0.15，那么每增加（减少）一个百分点的波动性，该期权的理论价值将增加（减少）0.15。如果该期权在 20% 波动性下的理论价值为 3.25，那么在 21% 波动性下，其理论价值将为 3.40，而在 19% 波动性下则为 3.10。

Note in Figure 6-20 that an at-the-money option always has a greater vega than either an in-the-money or out-of-the-money option when all options are of the same type and have the same amount of time to expiration. This means that an at-the-money option is always the most sensitive in total points to a change in volatility. As a corollary, the out-of-the-money option is always the most sensitive in percent terms to a change in volatility. For example, suppose that with a volatility assumption of 15% an at-the-money and an out-of-the-money option have theoretical values of 2.00 and .50, respectively. If we raise our volatility assumption to 20%, the options might now have theoretical values of 3.00 and 1.00. The at-the-money option has shown the greater total point increase (1.00 vs. .50), while the out-of-the-money option has shown the greater percent increase (50% vs. 100%. Since many option strategies involve buying and selling unequal numbers of options, the latter characteristic will be important when we look at trading strategies. (The reader can confirm this by looking again at Figure 4-11.) Note also in Figure 6-20 that the vega of all options declines as expiration approaches. Therefore, a long-term option will always be more sensitive to a change in volatility than a short-term option with otherwise identical contract specifications. A four month option will have a greater vega, and therefore be more sensitive to a change in volatility, than a one-month option.

在图 6-20 中可以看到，当所有期权类型相同且剩余到期时间相同时，平值期权的维加总是大于深度实值期权和深度虚值期权。这意味着平值期权对波动性变化的总点数反应最为敏感。相应地，深度虚值期权在波动性变化中在百分比上最为敏感。例如，假设在 15% 的波动性假设下，平值期权和深度虚值期权的理论价值分别为 2.00 和 0.50。如果我们将波动性假设提高到 20%，这两个期权的理论价值可能分别变为 3.00 和 1.00。平值期权的总点数增加更大（1.00 对 0.50），而深度虚值期权的百分比增加更大（50% 对 100%）。许多期权策略涉及买入和卖出不等数量的期权，因此这种特征在研究交易策略时将很重要。（读者可以再次查看图 4-11 以确认这一点。）此外，在图 6-20 中还可以看到，随着到期日的临近，所有期权的维加都会下降。因此，长期期权对波动性变化的敏感度总是高于短期期权，前提是其他合约规格相同。四个月的期权比一个月的期权具有更大的维加，因此对波动性变化更为敏感。

This last point illustrates an important principle of option evaluation, that time and volatility are closely interconnected. More time to expiration means more time for volatility to take effect, while less time to expiration may mean that any change in volatility will have only a minor effect on an option's value. Moreover, changes in the amount of time remaining to expiration and changes in volatility often have similar effects on an option's value. Decreasing volatility is similar to decreasing time to expiration. If a trader cannot remember what effect the passage of time will have on his position, he might consider instead what effect a reduction in volatility will have. This can be seen by comparing Figures 6-15 and 6-18 (theoretical values with respect to changes in time and volatility), Figures 6-11 and 6-13 (delta values with respect to changes in time and volatility), and Figures 6-9 and 6-10 (gamma values with respect to changes in time and volatility). In each case the similar shapes of the graphs indicate similar effects of time and volatility.

最后一点说明了期权评估的一个重要原则，即时间和波动性密切相关。到期时间越长，波动性发挥作用的时间就越多；而到期时间越短，波动性变化对期权价值的影响可能会较小。此外，剩余到期时间的变化和波动性的变化对期权价值的影响往往是相似的。波动性降低类似于到期时间减少。如果交易者无法记住时间流逝对其头寸的影响，可以考虑波动性降低的效果。这一点可以通过比较图 6-15 和图 6-18（与时间和波动性变化相关的理论价值）、图 6-11 和图 6-13（与时间和波动性变化相关的德尔塔值），以及图 6-9 和图 6-10（与时间和波动性变化相关的伽马值）来观察。在每种情况下，图形的相似形状表明时间和波动性有类似的影响。

Finally, we can see in Figure 6-21 that the vega of an at-the-money option is relatively constant, regardless of changes in volatility. This makes it easy to estimate the theoretical value of an at-the-money option under a wide variety of volatility scenarios.

最后，我们可以在图 6-21 中看到，平值期权的西塔在波动性变化时相对稳定。这使得在多种波动性情景下，估算平值期权的理论价值变得简单。

THE RHO
罗（rho）

The sensitivity of an option's theoretical value to a change in interest rates is given by its rho (P). Unlike the other sensitivities, one cannot generalize about the rho since its characteristics depend on the type of underlying instrument and the settlement proce dure for the options. The general effects have already been summarized in Figure 6-2.

期权理论价值对利率变化的敏感度由其 “罗”（ρ）表示。与其他敏感度不同，不能对 “罗” 进行一般化，因为它的特性取决于基础工具的类型和期权的结算程序。一般效应已在图 6-2 中总结。

Note that foreign currency options which require the delivery of the currency, rather than the delivery of a futures contract, are affected by both domestic and foreign interest rates. Hence, such options have two interest rate sensitivities, rho, (the domestic interest rate sensitivity) and rho, (the foreign interest rate sensitivity). The latter is sometimes denoted with the Greek letter phi (Ф).

请注意，外币期权需要交付货币，而不是交付期货合约，因此受到国内和国外利率的影响。因此，这类期权具有两个利率敏感度：罗（ρ₁，国内利率敏感度）和罗（ρ₂，国外利率敏感度）。后者有时用希腊字母 “phi”（Ф）表示。

If both the underlying contract and options are subject to futures-type settlement, the tho must be zero, since no cash flow results from either a trade in the underlying contract or a trade in the options. When options on futures are subject to stock-type settlement, the rho associated with both calls and puts is negative. An increase in interest rates will decrease the value of such options since it raises the cost of carrying the options. In the case of stock options, calls will have positive rhos (an increase in interest rates will make calls a more desirable alternative to buying the stock) and puts will have negative rhos (an increase in interest rates will make puts a less desirable alternative to selling the stock).

如果标的合约和期权都采用期货型结算，则 “罗” 必须为零，因为无论是标的合约的交易还是期权的交易都不会产生现金流。当期货期权采用股票型结算时，买权和卖权的 “罗” 都是负值。利率上升会降低这些期权的价值，因为这增加了持有期权的成本。在股票期权的情况下，买权的 “罗” 为正（利率上升会使买权比直接购买股票更具吸引力），而卖权的 “罗” 为负（利率上升会使卖权比直接出售股票更不具吸引力）。

Although changes in interest rates can affect an option's theoretical value, the interest rate is usually the least important of the inputs into a pricing model. For this reason the rho usually takes a back seat to the other, more critical, sensitivities: the delta, gamma, theta, and vega. Indeed, few traders pay much attention to the rho. However, for completeness, some of the characteristics of the rho are shown in Figures 6-22 futures options) and 6-23 (&stock options). In all cases the options which have the highest rho are those which are deeply in-the-money, because they require the greatest cash outlay.

尽管利率变化会影响期权的理论价值，但在定价模型中，利率通常是最不重要的输入因素。因此，“罗” 通常在其他更关键的敏感度（如 “德尔塔”、“伽马”、“西塔” 以及 “维加”）之后。实际上，很少有交易者对 “罗” 给予太多关注。不过，为了完整性，图 6-22（期货期权）和图 6-23（股票期权）展示了一些 “罗” 的特征。在所有情况下，“罗” 最高的期权通常是深度实值期权，因为它们需要更大的现金支出。

And the greater the amount of time to expiration, the greater the rho. Note also that because an option is a substitute for a position in the underlying instrument, the rho for stock options is much greater in magnitude than the rho for futures options. The purchase or sale of stock results in a much greater cash flow than the purchase or sale of a futures contract. (The vertical scale in Figure 6-23 is approximately ten times greater than the vertical scale in Figure 6-22.) Because of its relatively minor importance, we will generally disregard the rho in analyzing option strategies and managing risk.

到期时间越长，“罗” 值越大。此外，由于期权可以替代基础工具的持仓，股票期权的 “罗” 值远大于期货期权的 “罗” 值。购买或出售股票所产生的现金流远大于购买或出售期货合约所产生的现金流。（图 6-23 的纵坐标大约是图 6-22 的纵坐标的十倍。）由于 “罗” 的相对重要性较低，我们在分析期权策略和管理风险时通常会忽略它。

SUMMARY
总结

It is important for the active option trader to become familiar with delta, gamma, theta, and vega characteristics, since he may need to make quick decisions about trading strategies and risk management, decisions which might well determine his financial fate. The following is a summary of these characteristics:

活跃的期权交易者需要熟悉 “德尔塔”、“伽马”、“西塔” 和 “维加” 的特性，因为这些特性可能影响他迅速做出交易策略和风险管理的决策，这些决策可能会影响他的财务状况。以下是这些特性的总结：

Delta-Deltas range from zero for far out-of-the-money calls to 100 for deeply in-the-money calls, and from zero for far out-of-the-money puts to -100 for deeply in-the-money puts.

At-the-money calls have deltas of approximately 50, and at-the-money puts approximately -50.

As time passes, or as we decrease our volatility assumption, call deltas move away from 50, and puts deltas away from -50. As we increase our volatility assumption, call deltas move towards 50, and put deltas towards -50.

Gamma-At-the-money options have greater gammas than either in- or out-of-the-money options with otherwise identical contract specifications.

As we increase our volatility assumption, the gamma of an in- or out-of-the-money option rises, while the gamma of an at-the-money option falls. As we decrease our volatility assumption, or as time to expiration grows shorter, the gamma of an in- or out-of-the money option falls, while the gamma of an at-the-money option rises, sometimes dramatically.

Theta-At-the-money options have greater thetas than either in- or out-of-the-money options with otherwise identical contract specifications.

The theta of an at-the-money option increases as expiration approaches. A short-term, at-the-money option will always decay more quickly than a long-term, at-the-money option.

As we increase (decrease) our volatility assumption, the theta of an option will rise (fall). Higher volatility means there is greater time value associated with the option, so that each day's decay will also be greater when no movement occurs.

Vega—At-the-money options have greater vegas than either in- or out-of-the-money options with otherwise identical contract specifications.

Out-of-the-money options have the greatest vega as a percent of theoretical value.

The vegas of all options decrease as time to expiration grows shorter. A long-term option is always more sensitive to a change in volatility than a short term option with otherwise identical contract specifications.

The vega of an at-the-money option is relatively constant with respect to changes in volatility. If we raise or lower volatility, the option's vega is unlikely to change significantly.

德尔塔：对于远期权，远离执行价的看涨期权德尔塔为零，而深度实值的看涨期权德尔塔为 100；远离执行价的看跌期权德尔塔为零，而深度实值的看跌期权德尔塔为 -100。

平值看涨期权的德尔塔约为 50，平值看跌期权的德尔塔约为 -50。

随着时间推移或降低波动率假设，买权的德尔塔会远离 50，卖权的德尔塔会远离 -50。当提高波动率假设时，买权的德尔塔向 50 靠拢，卖权的德尔塔也向 -50 靠拢。

伽马：平值期权的伽马大于具有相同合约特征的实值或虚值期权。

随着波动率假设的提高，虚值或实值期权的伽马上升，而平值期权的伽马下降。随着波动率假设的降低或到期时间的缩短，虚值或实值期权的伽马下降，而平值期权的伽马上升，有时显著增加。

西塔：平值期权的西塔大于具有相同合约特征的实值或虚值期权。

平值期权的西塔随着到期日的临近而增加。短期平值期权的价值衰减快于长期平值期权。

提高（降低）波动率假设时，期权的西塔会增加（减少）。较高的波动率意味着期权的时间价值更高，因此在没有价格变动的情况下，每天的衰减也会更大。

维加：平值期权的维加大于具有相同合约特征的实值或虚值期权。

虚值期权的维加在理论价值中占比最大。

随着到期时间的缩短，所有期权的维加都会下降。长期期权对于波动率变化的敏感性总是高于短期期权，尽管其他合约特征相同。

平值期权的维加对于波动率变化相对恒定。如果提高或降低波动率，期权的维加不太可能发生显著变化。

In Figure 6-3 we summarized the general effects on stock option values if the expected dividend payment for the underlying stock changes. But we did not address the question of magnitude. How sensitive is an option's value to a change in dividends? When a stock goes ex-dividend, its price will normally drop by approximately the amount of the dividend. Increasing the dividend is therefore similar to dropping the stock price, and cutting the dividend is similar to increasing the stock price. If a stock had been expected to pay a dividend of $.75 per share, and the dividend is increased to $1.00 per share, this is similar to dropping the stock price by an additional $.25. Since an option's sensitivity to a change in the price of the underlying is given by the delta, the sensitivity to a change in the dividend can also be approximated by the delta. If the dividend is increased by $.25, a call with a delta of 60 will lose about $.15 in value. A put with a delta of -40 will gain about $.10. This approximation applies only when one dividend payment is expected prior to expiration. If multiple dividend payments are expected over the life of the option, the effect on the option's value must be increased accordingly. As we will see, dividend considerations play their greatest role in arbitrage strategies and early exercise.

在图 6-3 中，我们总结了预期股息支付变动对股票期权价值的一般影响，但没有讨论其幅度。期权的价值对股息变化的敏感性如何？当股票除息时，其价格通常会下降大约与股息相等的金额。因此，增加股息类似于降低股票价格，削减股息则类似于提高股票价格。例如，如果预期每股股息为 0.75 元，而股息增加到 1.00 元，这就相当于股票价格额外下降 0.25 元。期权对标的资产价格变动的敏感性由德尔塔决定，因此对股息变化的敏感性也可以用德尔塔来近似。如果股息增加 0.25 元，德尔塔为 60 的看涨期权将损失约 0.15 元的价值，而德尔塔为 -40 的看跌期权将增加约 0.10 元的价值。这种近似只适用于到期前预期的单次股息支付。如果期权的有效期内预计有多次股息支付，则对期权价值的影响需相应增加。如我们所见，股息因素在套利策略和提前行权中发挥着重要作用。

Two typical evaluation tables with prices, implied volatilities, and all relevant sensitivities are shown in Figures 6-24 and 6-25. Figure 6-24 is for options on September Deutschemark futures on the Chicago Mercantile Exchange as of 22 May 1992. The values are based on a volatility assumption of 10.5% and an interest rate assumption of 4.50%. Figure 6-25 is for options on General Electric stock on the Chicago Board Options Exchange as of the same date. The values are based on a volatility assumption of 22% and an interest rate assumption of 4.50% for all three expiration months (une, September, December). (footnote 6: This is a simplified example with untform volatility and interest rates. Under some circumstances it might be more reasonable to vary the volatility and interest rate assumptions for different expiration) The expected dividends for General Electric stock, and their payment dates, are also included in the assumptions. (footnote 7: Due to the greater likelihood of early exercise for stock options, and the fact that the quoted options are American, the calculations in Figure 6-25 were done using a binomial model, which more accurately evaluates the early exercise value of American options. The problem of early exercise will be discussed further in Chapter 12.)

图 6-24 和图 6-25 展示了两份典型的评估表，包含价格、隐含波动率和所有相关的敏感性。图 6-24 为 1992 年 5 月 22 日芝加哥商业交易所的 9 月德国马克期货期权，数值基于 10.5% 的波动率假设和 4.50% 的利率假设。（脚注 6：这是一个简化的例子，假设波动率和利率均为统一值。在某些情况下，为不同到期日变化波动率和利率假设可能更合理。）通用电气股票的预期股息及其支付日期也包含在假设中。图 6-25 为同日芝加哥期权交易所的通用电气股票期权，数值基于 22% 的波动率假设和 4.50% 的利率假设，适用于所有三个到期月份（6 月、9 月、12 月）。（脚注 7：由于股票期权早期行权的可能性较大，以及所引用的期权为美式期权，图 6-25 中的计算采用了二项模型，以更准确地评估美式期权的早期行权价值。有关早期行权的问题将在第 12 章进一步讨论。）

We noted previously that the delta, gamma, theta, and vega can be sensitive to changes in volatility. Under some circumstances it may be useful for a trader to ask: if the implied volatility of an option were the correct volatility, what would be its delta, gamma, theta, and vega? The resulting numbers are referred to as the implied delta, gamma, theta, and vega. The implied delta and theta, in particular, often appear on computer printouts, the former because many traders prefer to maintain delta neutral positions using the implied delta, and the latter because the rate at which the price of an option decays is usually more useful than the rate at which the theoretical value decays.

我们之前提到，德尔塔、伽马、西塔和维加对波动率的变化很敏感。在某些情况下，交易者可能会问：如果期权的隐含波动率是正确的，那么它的德尔塔、伽马、西塔和维加是多少？由此得出的数字称为隐含德尔塔、隐含伽马、隐含西塔和隐含维加。尤其是隐含德尔塔和隐含西塔，通常会出现在电脑打印输出中，前者因为许多交易者倾向于使用隐含德尔塔来维持德尔塔中性头寸，后者因为期权价格的衰减速率通常比理论价值的衰减速率更有用。

Knowing the total delta, gamma, theta, and vega of an option position can help a trader determine beforehand how the position is likely to react to changing market conditions. Since all these numbers are additive, the total sensitivity of a position can be calculated by adding up the sensitivities of the individual options. For example, a trader who has purchased five options with a gamma of 2.5 each, and sold two options with a gamma of 4.0 each, has a total gamma position of

(+5×2.5) + (-2 × 4.0) = +4.5

Similarly, if he has purchased nine options with a theta of -05 each, and sold four options with a theta of -08 each, his total theta position is

(+9 x-05) + (-4×-.08) = -13

了解一个期权头寸的总德尔塔、伽马、西塔和维加可以帮助交易者提前判断该头寸在市场条件变化时的反应。由于这些数值都是可加的，头寸的总敏感性可以通过将各个期权的敏感性相加来计算。例如，一个交易者购买了五个每个伽马为 2.5 的期权，同时卖出了两个每个伽马为 4.0 的期权，那么他的总伽马头寸为：

(+5×2.5) + (-2×4.0) = +4.5

同样，如果他购买了九个每个西塔为 -0.5 的期权，并卖出了四个每个西塔为 -0.8 的期权，那么他的总西塔头寸为：

(+9×-0.5) + (-4×-0.8) = -1.3

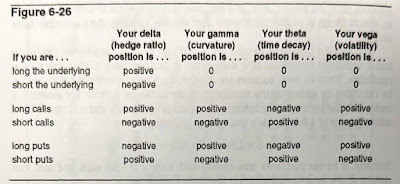
New traders sometimes find it difficult to remember whether a delta, gamma, theta, or vega position is long or short. The various positions and their respective signs are given in Figure 6-26. The sign of the delta, gamma, theta, or vega, together with the magnitude of the numbers, tell the trader which changes in market conditions will either help or hurt his position, and to what degree. The positive or negative effect of changing market conditions is summarized in Figure 6-27.

 

新手交易者有时会难以记住某个德尔塔、伽马、西塔或维加头寸是多头还是空头。各种头寸及其符号见图 6-26。德尔塔、伽马、西塔或维加的符号及数值的大小，可以告诉交易者在市场条件变化时哪些变化会对其头寸有利或不利，以及影响的程度。市场条件变化的正负影响在图 6-27 中进行了总结。

Even though a trader can analyze the effect of changing market conditions on his position through its delta, gamma, theta, and vega characteristics, his first and primary concern is that the position be profitable if his assumptions about market conditions are correct. This means that the position ought to have a positive theoretical edge. The theoretical edge can be calculated in the same way as the total delta, gamma, theta, and vega. One need only multiply the theoretical edge of each individual option (the difference between its trade or settlement price and theoretical value) by the number of contracts traded, and add up all the contracts involved. The amount of positive or negative theoretical edge is a reflection of the position's potential profit or loss.

尽管交易者可以通过德尔塔、伽马、西塔和维加特征分析市场条件变化对其头寸的影响，但他最关心的仍然是如果对市场条件的假设正确，该头寸是否能盈利。这意味着该头寸应具有正的理论优势。理论优势可以通过与总德尔塔、伽马、西塔和维加相同的方式计算。只需将每个单独期权的理论优势（其成交或结算价格与理论价值之间的差）乘以交易的合约数量，然后将所有合约的结果相加即可。正的或负的理论优势反映了该头寸的潜在利润或损失。

The top portion of Figure 6-28 shows a theoretical evaluation table for individual options on a hypothetical futures contract. Beneath the table are several possible option positions for which the total theoretical edge, delta, gamma, theta, and vega have been calculated. The reader should take a moment to look at the arithmetic of each position, and to consider the risk characteristics associated with each position. Are all the positions likely to be profitable if the assumptions used for theoretical evaluation are correct? What will help or hurt each position?

图 6-28 的上半部分展示了一个假设期货合约的单个期权的理论评估表。表下方列出了几个可能的期权头寸，并计算了它们的总理论优势、德尔塔、伽马、西塔和维加。读者应花一点时间查看每个头寸的计算，并考虑与之相关的风险特征。如果用于理论评估的假设正确，所有头寸是否都可能盈利？什么因素会影响每个头寸的收益？

There is one other option sensitivity that is not generally used by traders, but which the reader may encounter in other option texts. An option's elasticity, sometimes denoted with the Greek letter omega (52) (or less commonly the Greek letter lambda(2), is the relative percent change in an option's value for a given percent change in the price of the underlying contract. For example, suppose a call has a theoretical value of 2.50 with the underlying contract at 50. If the call has a delta of 25, and the underlying contract rises one point to 51, the call should rise to 2.75. In percent terms the call has changed its value five times as fast as the underlying: the underlying rose 2% (1/50), while the call rose 10% (.25/2.50). We say that the call has an elasticity of 5. The elasticity is sometimes referred to as the option's leverage value. The greater an option's elasticity, the more highly leveraged the option.

还有一种期权敏感性通常不被交易者使用，但读者可能会在其他期权书籍中遇到。这种敏感性称为期权的弹性，有时用希腊字母Ω（omega）表示（或较少使用希腊字母λ（lambda））。期权的弹性是期权价值对标的合约价格变动的相对百分比变化。例如，假设一个看涨期权的理论价值为 2.50，标的合约价格为 50。如果该看涨期权的德尔塔为 25，标的合约价格上涨 1 点至 51，那么该看涨期权的价值应上涨至 2.75。以百分比计算，该看涨期权的价值变化速度是标的合约的五倍：标的合约上涨了 2%（1/50），而看涨期权上涨了 10%（0.25/2.50）。我们称该看涨期权的弹性为 5。弹性有时也被称为期权的杠杆值。期权的弹性越大，其杠杆作用越明显。

An easy method of calculating an option's elasticity is to divide the price of the underlying contract by the option's theoretical value, and multiply this by the option's delta when calculating the elasticity, we use the decimal format for the delta):

elasticity = underlying price / theoretical value × delta

In our example we have:

elasticity = 50 / 2.50 × .25 = 5

计算期权弹性的一种简单方法是将标的合约的价格除以期权的理论价值，然后再乘以期权的德尔塔（在计算弹性时，德尔塔使用小数格式）：

弹性 = 标的价格 / 理论价值 × 德尔塔

在我们的例子中：

弹性 = 50 / 2.50 × 0.25 = 5

One final observation for the prospective trader. All the numbers we have discussed in this chapter, the theoretical value, delta, gamma, theta, vega, and tho, are constanty changing, so that the profitability and risks associated with different strategies are also changing. The importance of analyzing risk cannot be overemphasized. The great majority of traders who fail at option trading do so because they fail to fully understand risk and how to manage it. But there is another type of trader, one who attempts to analyze every possible risk. When this happens, the trader finds it difficult to make any trading decisions at all; he is stricken with paralysis through analysis. A trader who is so concerned with risk that he is afraid to make a trade cannot profit, no matter how well he understands options. When a trader goes into the marketplace he has chosen to take on some risk. The delta gamma, theta, and vega enable him to identify risk; they do not eliminate risk. The intelligent trader uses these numbers to help him decide beforehand which risks are acceptable and which risks are not.

最后，给潜在交易者的一个观察：本章讨论的所有数据，包括理论价值、德尔塔、伽玛、希塔、维加和西塔，都在不断变化，因此不同策略的盈利能力和风险也在变化。分析风险的重要性不容忽视。大多数在期权交易中失败的交易者，往往是因为未能充分理解风险及其管理方式。但还有另一类交易者，他们试图分析每一种可能的风险。当这种情况发生时，交易者会发现自己难以做出任何交易决策，陷入 “分析瘫痪”。一个过于担心风险、害怕交易的交易者，无论对期权的理解有多深，都无法获利。当交易者进入市场时，他已选择承担一定风险。德尔塔、伽玛、希塔和维加帮助他识别风险，而非消除风险。聪明的交易者利用这些数据提前判断哪些风险可接受，哪些不可接受。